Filtro kalman

«El cálculo es el lenguaje con el cual Dios ha escrito el universo.»

Galileo Galilei

El filtro de Kalman es un algoritmo desarrollado por Rudolf E.Kalman en 1960 usado para estimar las variables de un sistema basándose en medidas con ruido. Lo que hace este algoritmo es calcular las diferentes probabilidades del estado del sistema, superponiéndolas posteriormente con las diferentes mediciones teniendo en cuenta su componente de ruido añadido. Es por ello que el filtro de Kalman es perfecto para usar sistemas embarcados donde las señales producidas por los sensores tienen incorporado abundante ruido para recoger la información del entorno.

Las variables de estado son el subconjunto más pequeño de variables de un sistema que pueden representar su estado dinámico completo en un determinado instante. De una manera intuitiva, las variables de estado contienen información suficiente para predecir el comportamiento futuro del sistema en ausencia de excitaciones externas.

El filtro Kalman es un algoritmo que requiere dos tipos de ecuaciones: las que relacionan las variables de estado con las variables observables (ecuaciones principales) y las que determinan la estructura temporal de las variables de estado (ecuaciones de estado).

Las estimaciones de las variables de estado se realizan en base a la dinámica de estas variables (dimensión temporal) así como de las mediciones de las variables observables que se van obteniendo en cada instante del tiempo (dimensión transversal).

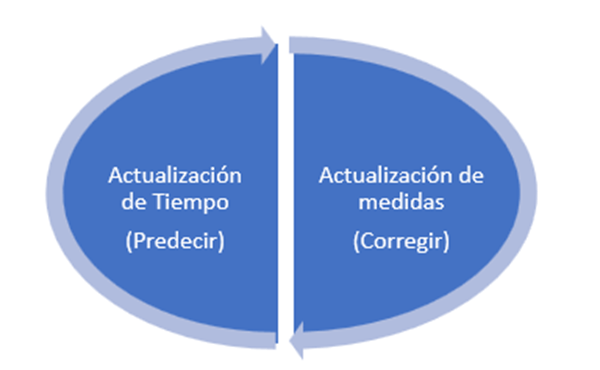
Es decir, la dinámica se resume en dos pasos:

1. Estimar las variables de estado utilizando su propia dinámica (etapa de predicción).
2. Mejorar esa primera estimación utilizando la información de las variables observables (etapa de corrección).

Para su mejor entendimiento y concebir la idea principal del fin de este filtro, suponemos el desarrollo del siguiente ejemplo:

Suponemos un niño en una bicicleta que se mueve en línea recta con un sensor de velocidad que no tiene error. Sabemos que el niño en bicicleta va a 3m/s y está a una distancia de 0m. Es decir que en 1 segundo el niño estará a 3m. Sin embargo, si no sabemos con exactitud la distancia a la que se encuentra el niño y además la velocidad no es 100% fiable las operaciones se complican.

Podemos usar las ecuaciones básicas del movimiento rectilíneo para el movimiento del vehículo a velocidad constante, suponiendo en este caso que se conoce la velocidad exacta del niño.

Sabemos que el vehículo se ha movido a una velocidad constante, por la tanto si dudamos si la posición inicial se encuentra entre -1 y 1 m también dudaremos si la posición final del niño al cabo de 1 segundo se encuentra entre 2 y 4 m. Se puede observar en la siguiente figura:

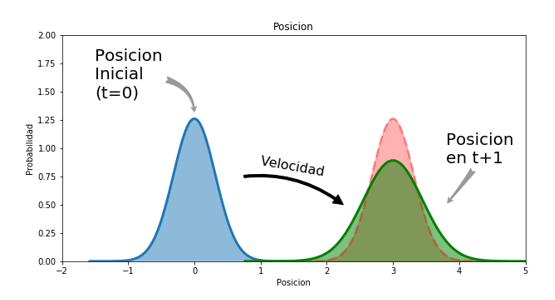
Ahora suponemos que todas las variables son aleatorias es decir que la velocidad del niño tampoco es segura:

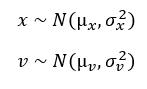
Si la velocidad como la posición son variables independientes, podemos calcular la media y la varianza de la nueva posición:

En la ecuación (iii) se puede concluir que al aumentar el tiempo la varianza de la nueva posición aumenta proporcionalmente a la varianza de la velocidad. Es decir, en cada instante que avanza el tiempo se tiene menos certeza de cuál es la verdadera posición del niño entonces se puede concluir que a medida que pasa el tiempo la varianza de la posición del niño aumenta. En la siguiente gráfica vemos la comparación para un tiempo idéntico como varia el resultado teniendo la velocidad fija o cuando esta contiene un componente de ruido aleatorio.

Con estos conceptos se puede predecir el siguiente estado y actualizar las variables aleatorias. Ahora se va a relacionar la predicción obtenida con los resultados de la medición.

Respecto a los resultados de la medición también se suponen que no son fiables, es decir también existe ruido en ellos, como si fueran una variable aleatoria más alrededor de la medición del sistema.

Con la medición obtenida por nuestro sensor y la predicción calculada anteriormente se puede reducir la probabilidad de la posición donde se encuentra la bicicleta.

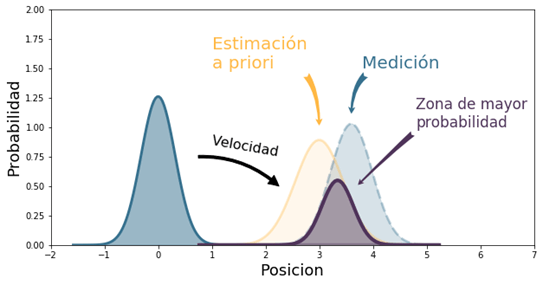
 Se supone que la medida obtenida m del sistema (el sensor que capta las mediciones) contiene ruido, por lo tanto, tampoco es fiable. Entonces necesitamos calcular cual es la posición más probable en función de la medición y la predicción.

Esta es la idea conceptual para disminuir la incertidumbre de la nueva posición. Los siguientes términos serán utilizados para conformar las ecuaciones del filtro.

• x: Vector con las variables del sistema
• A: Matriz de predicción del siguiente estado
• B: Matriz de entradas externas al sistema
• u: Vector de entradas
• P_k: es la matriz de covarianza de nuestra variable de estado en el instante k
• Q_k: es el ruido que añade el entorno a nuestro sistema.

La matriz P estará formada en la diagonal principal por las varianzas de cada uno de los estados de nuestro vector de estado y fuera de la diagonal principal, estarán las covarianzas entre las diferentes variables.

La matriz H asocia el estado del sistema con las medidas de los sensores. Es decir, en el caso que el vector con las variables x tenga las variables de posición y velocidad (x = [posición; velocidad]), la matriz H si queremos medir únicamente la posición será:

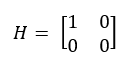
En cambio, si las mediciones que obtenemos son de velocidad y tiempo, la matriz será:

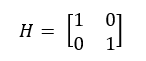
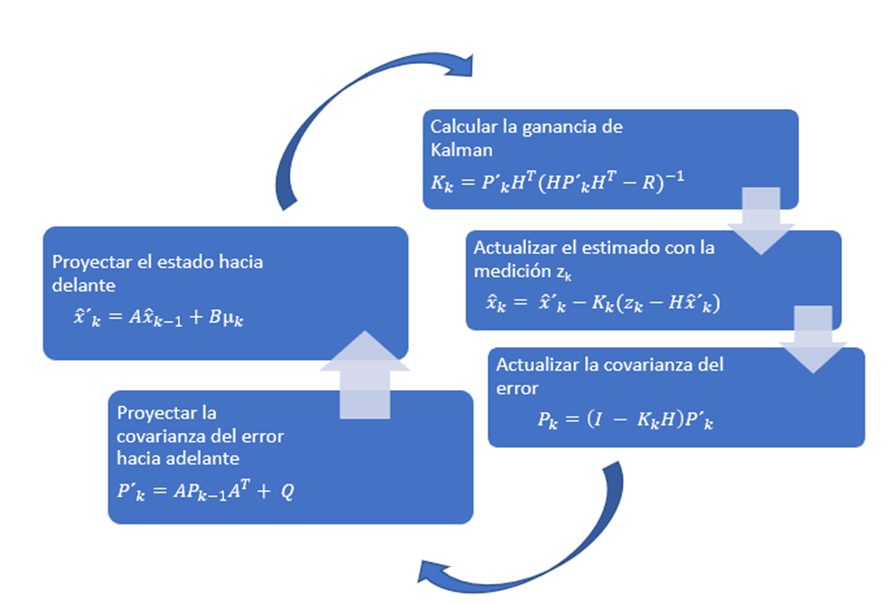
El algoritmo de Kalman se calcula únicamente con 5 ecuaciones en dos etapas, la etapa de predicción que contiene dos ecuaciones y la etapa de corrección que contiene tres. Estas ecuaciones son las siguientes:

Es importante que encada iteración se haga una reasignación de variables

como se muestra a continuación:                       

Este es una pequeña explicación de este filtro que es útil para filtrar muchas de las señales provenientes de los sensores utilizados por muchos de los sistemas armamentísticos de la actualidad.

Gracias por su atención y un abrazo de parte del equipo de ElectroBlindado.com